浅谈TypeScript的图灵完备性
Nov 19, 2022typescript浅谈 TypeScript 的图灵完备性
一、图灵完备
1.图灵完备的概念
首先从定义出发,什么是图灵完备:图灵完备指一系列操作数据的规则能够模拟任何图灵机。
WikiPedia-图灵完备介绍,在可计算性理论,如果一系列操作数据的规则(如指令集、编程语言、细胞自动机)可以用来模拟任何图灵机,那么它是图灵完备的。这意味着这个系统也可以识别其他数据处理规则集,图灵完备性被用作表达这种数据处理规则集的一种属性。
1.1 图灵等价
还有一个相关概念是图灵等价: 如果 P 可以模拟 Q 并且 Q 可以模拟 P,则两台计算机 P 和 Q 称为等效计算机。
邱奇-图灵论题认为任何可以通过算法计算其值的函数都可以由图灵机计算,因此,如果任何真实世界的计算机都可以模拟图灵机,则其对图灵机是图灵等价的。 通用图灵机可用于模拟任何图灵机,且可以扩展现实世界计算机的计算方面。
如果某物是图灵完备的,则它可以用于模拟某些图灵完备的系统。
2.图灵机和可计算函数
2.1 图灵机
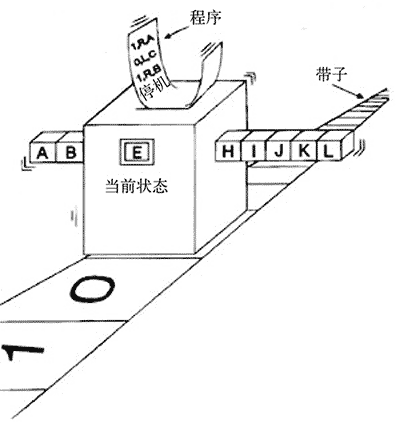
如上图,图灵机由艾伦·麦席森·图灵1936 年提出,它是一个虚拟机器,可模拟计算机的任何算法,无论算法多么复杂。
在 1928 年第八届国际数学家大会上,德国数学家希尔伯特(David Hilbert,1862 - 1943)提出了关于数学的三个精辟问题:
1 | First, was mathematics complete ...(数学是完备的吗?) |
希尔伯特的第三个问题又被称为判定性问题(Entscheidungsproblem)。为了证否这个命题,1936 年,图灵发表了一篇论文,题为《论可计算数,及其在判定性问题上的应用》(On Computable Numbers, with an Application to the Entscheidungsproblem)。在这篇论文里,图灵提出了一种假设的计算装置,他称之为 A-Machine(Automatic Machine,自动机器),这就是图灵机(Turing Machine)。
关于图灵机具体运作及 Brainfuck 语言的内容本文不做整理,可以看WikiPedia-图灵机介绍,WikiPedia-Brainfuck
2.2 可计算函数
A function is effectively calculable if its values can be found by some purely mechanical process.
图灵定义了一类被称为“可计算函数”的数学函数,它们可以被图灵机计算。图灵机的计算模型被认为是一种形式化的计算模型,可以模拟所有的可计算函数,这意味着如果一个函数可以被计算,那么它一定可以被图灵机计算。
在作为特定计算模型的图灵机上产生的可计算函数,就被称为图灵可计算函数。
3.图灵完备语言
具有图灵完备性的计算机语言,就被称为图灵完备语言。如今,几乎所有编程语言都具有图灵完备性。
一个语言被称为图灵完备语言,需要满足以下几个要求或特征:
- 具有基本算数和逻辑运算功能,例如加减乘除、布尔运算、比较等。
- 可以实现条件判断和循环操作,例如 if-else 语句、while 循环等。
- 具备无限循环能力,以便模拟图灵机。
- 可以进行任意长度的计算和存储数据,以便模拟图灵机。
- 支持函数或过程调用和递归,以便模拟复杂计算。
它意味着任何实现以下八条指令的机器都是一台计算机(因此可以执行任何种类的计算)。
.,: 输入或输出一个指令+-: 加或减内存中的值><: 将当前的指针向左或向右移动。[]: 执行循环
实际上,如果某种语言可以执行以上八种指令,就可以称为是图灵完备的。
证明我们可以(用这个程序语言)模拟一个图灵机是一个证明语言图灵完备性的好方法,但这不是唯一的方法,另一种方法是证明你的语言能够描述所有的μ-recursive functions。
广泛使用的所有通用语言:
- 过程式语言,如 FORTRAN、Pascal 等。
- 面向对象语言,如 Java、Python、JavaScript 等。
- 多范式语言,如 Ada、C++ 等。
使用不太常见范式的大多数语言:
- 函数式语言,如 Haskell、Mercury 等。
- 逻辑式语言,如 Logtalk、Prolog 等。
- 声明式语言,如 SQL、XSLT 等。
- 深奥的语言(Esoteric Programming Language),一种奇特的数学娱乐形式,程序员用极其困难但数学上图灵等价的语言来实现基本的编程结构。
注意,一个语言的图灵完备性只与它的语法和语义相关,而与其具体实现或运行环境无关。因此,同一种语言在不同的平台上可能会有不同的图灵完备性。
4.非图灵完备语言
并非所有的计算机语言都是图灵完备的,例如标记语言,或者更恰当地称为“容器语言”或“数据描述语言”,就不是图灵完备的。
非图灵完备语言(Non-Turing-Complete Language),包括 HTML、JSON、XML、YAML、正则表达式 等。
需要注意的是,尽管这些语言不是图灵完备的,但它们仍然具有实际应用价值。
5.图灵完备的应用和意义
数学家们早已经提出了邱奇-图灵论题以概括图灵机的计算能力,任何可计算过程都可以用图灵机来模拟。这是一个论题而非定理,因为它实际上是对可计算过程的定义,而非证明。但迄今为止,人们尚未发现一个可以视为计算的过程是图灵机不能模拟的。
图灵完备性也可以用来描述计算机语言的计算能力,如果一门语言图灵完备,这就意味着这门语言可以做到能够用图灵机能做到的所有事情,可以解决所有的可计算问题。
6.其他
进行程序计算的一定是图灵完备的,图灵完备的不一定能进行程序计算。
二、TypeScript 的图灵完备性
TypeScript 是一种由微软开发的编程语言, 是 JavaScript 的超集,具有静态类型系统。
Typescript 空间分为类型空间和值空间。两个空间不互通,因此值不能当成类型,类型不能当成值,并且值和类型不能做运算等。因此我们需要分别考虑类型空间和值空间的图灵完备性:
1.TypeScript 的图灵完备性验证
1.1 Type System Encoding 方法
Type System Encoding 是一种通过利用类型系统来实现计算的方法。它基于一个简单的思想,即使用类型来表示值的结构和意义。在 Type System Encoding 中,程序的行为是由类型的变化所驱动的。
以下是一个可能的 Type System Encoding 方法的实现步骤:
- 1.定义类型系统。要实现 Type System Encoding,首先需要一个类型系统。可以选择现有的类型系统,如 lambda 演算,或者根据需要定义一个新的类型系统。
- 2.定义类型。定义类型是 Type System Encoding 的核心,因为它决定了如何表示值和如何执行操作。可以使用基本类型,如整数和布尔值,也可以使用自定义类型,如列表和树。
- 3.定义类型之间的转换。在 Type System Encoding 中,程序的执行通常涉及类型之间的转换。因此,需要定义如何将一个类型转换为另一个类型。可以使用类型转换函数,也可以使用类型转换规则。
- 4.定义类型操作。要实现 Type System Encoding,需要定义一组操作,这些操作涉及类型的创建、转换和组合。可以使用一些基本操作,如 lambda 抽象和应用,也可以使用自定义操作。
- 5.编写程序。完成上述步骤之后,可以开始编写程序。程序可以使用定义的类型和操作来实现所需的功能。在程序执行期间,类型之间的转换将驱动程序的行为。
通过 Type System Encoding 方法,可以将程序的控制流与类型系统相结合,从而实现程序的计算。Type System Encoding 方法的一个优点是,它可以提供静态类型检查和类型推断,从而减少程序错误的可能性。此外,Type System Encoding 方法还可以提供一些有用的抽象和模块化机制,使得程序更易于维护和重用。
使用 Type System Encoding 方法,我们可以验证 TypeScript 是否具有图灵完备性。
1.2 类型系统的图灵完备验证
早在 2017 年,TypeScript 的 github 上就有人提出 ts2.2 类型系统是图灵完备的,楼主也给出了相关证明,此 issue 也引发了大量讨论(https://github.com/Microsoft/TypeScript/issues/14833)。
我们知道,TypeScript 类型系统是“独立”于值系统的存在,我们可以通过映射类型、递归类型定义、索引访问成员类型以及可以创建任意数量的类型,来实现图灵完备。
如下,当 TrueExpr、FalseExpr 和 Test 定义为适合的类型,如下的实现将具备图灵完备性:
1 | type MyFunc<TArg> = { |
TypeScript 包含了一套完整的类型层面编程能力,就像我们可以用 JavaScript、C++、Go 等编程语言解决各种实际问题一样,TypeScript 可以解决各种类型问题,因为本质上它们的内核都和图灵机等价。
由此 TypeScript 开发者可以自由发挥类型作用,比如开发判定素数的类型 IsPrime<T> 、将合集类型转换为元组的类型 UnionToTuple<T>、根据条件获取子集类型的类型 ConditionalSubset<T> 等等、即 TypeScript 类型编程。
比如IsPrime:
1 | function isPrime(number: number): boolean { |
2.类型编程的花式操作
TypeScript 类型的图灵完备性证明意味着它具备了与其他图灵完备语言相同的计算能力,可以在理论上执行任何可计算的操作。
2.1 用 ts 类型系统写象棋

效果体验:https://tsplay.dev/Nd4n0N
具体实现可见:《用 TypeScript 类型运算实现一个中国象棋程序》
2.2 用 ts 类型系统写一个 Lisp 解释器
在 ts 写象棋的引领下,ts 花式操作越来越多,像扫雷等等,甚至有人用于写解释器。
见:https://zhuanlan.zhihu.com/p/427309936
*type-challenges
要写出象棋这种花式操作、或者本质来说学好 ts 类型知识,我们需要大量的实践和理解,在这type-challenges就是一个很好的实践类学习项目,此项目通过刷题让你更好的了解 TS 的类型系统,编写你自己的类型工具。
3.ts 值空间图灵完备验证
相比类型系统,ts 的值空间图灵完备验证就很容易,即 JavaScript 的图灵完备性验证。
正因为 js 具备图灵完备性,因此像微信无法从根本上禁止小程序代码的热更,因为我们可以根据宿主语言(js)实现任何其他图灵完备的编程语言。比如 用 js 实现 js 解释器、Python 解释器、PHP 解释器等等,甚至你还可以设计一个自己的比如本文的字节码虚拟机。
对微信小程序禁止 eval 热更的讨论感兴趣可以看官方社区——关于禁止小程序 JavaScript 解释器使用规范要求
三、最后
ts 类型系统具备图灵完备,虽然用 ts 类型系统写复杂逻辑没有太大意义,但我们也能看到 ts 能做的事越来越多、对于 ts 开发者的使用也越来越灵活方便。
最后,致敬艾伦·麦席森·图灵(Alan Mathison Turing,1912.6.23 - 1954.6.7),英国数学家、逻辑学家、密码学家和英国首位计算机科学家,被誉为计算机科学和人工智能之父。

另外,可以思考一下,现在的 CSS 是图灵完备的语言吗?
相关链接
- https://zh.m.wikipedia.org/zh-cn/%E5%9C%96%E9%9D%88%E5%AE%8C%E5%82%99%E6%80%A7
- https://github.com/Microsoft/TypeScript/issues/14833
- 《用 TypeScript 实现汉诺塔》
- 《用 TypeScript 类型运算实现一个中国象棋程序》
- 《TypeScript 类型体操天花板,用类型运算写一个 Lisp 解释器》
- 《【🤦♂️ 工作无用】证明 JS 和 TS 类型编程是图灵完备的》
- https://zh.wikipedia.org/wiki/%E8%89%BE%E4%BC%A6%C2%B7%E5%9B%BE%E7%81%B5
- https://developers.weixin.qq.com/community/minihome/doc/0000ae500e4fd0541f2ea33755b801
Author
My name is Micheal Wayne and this is my blog.
I am a front-end software engineer.
Contact: michealwayne@163.com