js中位运算的骚操作
Oct 29, 2019笔记jsesjs中位运算的骚操作
按位操作符
按位操作符(Bitwise operators) 将其操作数(operands)当作32位的比特序列(由0和1组成),而不是十进制、十六进制或八进制数值。
| 运算符 | 用法 | 描述 |
|---|---|---|
| 按位与(AND) | a & b | 对于每一个比特位,只有两个操作数相应的比特位都是1时,结果才为1,否则为0。 |
| 按位或(OR) | a ¦ b | 对于每一个比特位,当两个操作数相应的比特位至少有一个1时,结果为1,否则为0。 |
| 按位异或(XOR) | a ^ b | 对于每一个比特位,当两个操作数相应的比特位有且只有一个1时,结果为1,否则为0。 |
| 按位非(NOT) | ~ a | 反转操作数的比特位,即0变成1,1变成0。 |
| 左移(Left shift) | a << b | 将 a 的二进制形式向左移 b (< 32) 比特位,右边用0填充。 |
| 有符号右移 | a >> b | 将 a 的二进制表示向右移 b (< 32) 位,丢弃被移出的位。 |
| 无符号右移 | a >>> b | 将 a 的二进制表示向右移 b (< 32) 位,丢弃被移出的位,并使用 0 在左侧填充。 |
有符号32位整数
所有的按位操作符的操作数都会被转成补码(two’s complement)形式的有符号32位整数。补码形式是指一个数的负对应值(negative counterpart)(如 5和-5)为数值的所有比特位反转后,再加1。反转比特位即该数值进行’非‘位运算,也即该数值的反码。例如下面为整数314的二进制编码:1
00000000000000000000000100111010
下面编码 ~314,即 314 的反码:1
11111111111111111111111011000101
最后,下面编码 -314,即 314 的反码再加1:1
11111111111111111111111011000110
补码保证了当一个数是正数时,其最左的比特位是0,当一个数是负数时,其最左的比特位是1。因此,最左边的比特位被称为符号位(sign bit)。
按位逻辑操作符
从概念上讲,按位逻辑操作符按遵守下面规则:
操作数被转换成32位整数,用比特序列(0和1组成)表示。超过32位的数字会被丢弃。例如, 以下具有32位以上的整数将转换为32位整数:
1
2转换前: 11100110111110100000000000000110000000000001
转换后: 10100000000000000110000000000001第一个操作数的每个比特位与第二个操作数的相应比特位匹配:第一位对应第一位,第二位对应第二位,以此类推。
位运算符应用到每对比特位,结果是新的比特值。
&(按位与)|(按位或)^(按位异或)~(按位非)
按位移动操作符
按位移动操作符有两个操作数:第一个是要被移动的数字,而第二个是要移动的长度。移动的方向根据操作符的不同而不同。
按位移动会先将操作数转换为大端字节序顺序(big-endian order)的32位整数,并返回与左操作数相同类型的结果。右操作数应小于 32位,否则只有最低 5 个字节会被使用。
注:Big-Endian:高位字节排放在内存的低地址端,低位字节排放在内存的高地址端,
又称为”高位编址”。
Big-Endian是最直观的字节序:
- ①把内存地址从左到右按照由低到高的顺序写出;
- ②把值按照通常的高位到低位的顺序写出;
- ③两者对照,一个字节一个字节的填充进去。
<< (左移)
该操作符会将第一个操作数向左移动指定的位数。向左被移出的位被丢弃,右侧用 0 补充。如:1
2
3 9 (base 10): 00000000000000000000000000001001 (base 2)
--------------------------------
9 << 2 (base 10): 00000000000000000000000000100100 (base 2) = 36 (base 10)
即9 << 2的值为36。
>> (有符号右移)
该操作符会将第一个操作数向右移动指定的位数。向右被移出的位被丢弃,拷贝最左侧的位以填充左侧。由于新的最左侧的位总是和以前相同,符号位没有被改变。所以被称作“符号传播”。1
2
3 9 (base 10): 00000000000000000000000000001001 (base 2)
--------------------------------
9 >> 2 (base 10): 00000000000000000000000000000010 (base 2) = 2 (base 10)
即9 >> 2得到 2。
1 | -9 (base 10): 11111111111111111111111111110111 (base 2) |
即-9 >> 2得到 -3。
>>> (无符号右移)
该操作符会将第一个操作数向右移动指定的位数。向右被移出的位被丢弃,左侧用0填充。因为符号位变成了 0,所以结果总是非负的。
对于非负数,有符号右移和无符号右移总是返回相同的结果。例如 9 >>> 2 和 9 >> 2 一样返回 2。
但是对于负数却不尽相同。 -9 >>> 2 产生 1073741821 这和 -9 >> 2 不同
标志位与掩码
位运算经常被用来创建、处理以及读取标志位序列——一种类似二进制的变量。虽然可以使用变量代替标志位序列,但是这样可以节省内存(1/32)。
例如,有 4 个标志位:
- 标志位 A:我们有 ant
- 标志位 B:我们有 bat
- 标志位 C:我们有 cat
- 标志位 D:我们有 duck
标志位通过位序列 DCBA 来表示。当一个位被置位 (set) 时,它的值为 1 。当被清除 (clear) 时,它的值为 0 。例如一个变量 flags 的二进制值为 0101:
1 | var flags = 5; // 二进制 0101 |
这个值表示:
- 标志位 A 是 true (我们有 ant);
- 标志位 B 是 false (我们没有 bat);
- 标志位 C 是 true (我们有 cat);
- 标志位 D 是 false (我们没有 duck);
因为位运算是 32 位的, 0101 实际上是 00000000000000000000000000000101。因为前面多余的 0 没有任何意义,所以他们可以被忽略。
掩码 (bitmask) 是一个通过与/或来读取标志位的位序列。典型的定义每个标志位的原语掩码如下:
1 | var FLAG_A = 1; // 0001 |
新的掩码可以在以上掩码上使用逻辑运算创建。例如,掩码 1011 可以通过 FLAG_A、FLAG_B 和 FLAG_D 逻辑或得到:
1 | var mask = FLAG_A | FLAG_B | FLAG_D; // 0001 | 0010 | 1000 => 1011 |
某个特定的位可以通过与掩码做逻辑与运算得到,通过与掩码的与运算可以去掉无关的位,得到特定的位。例如,掩码 0100 可以用来检查标志位 C 是否被置位:
1 | // 如果我们有 cat |
一个有多个位被置位的掩码表达任一/或者的含义。例如,以下两个表达是等价的:
1 | // 如果我们有 bat 或者 cat 至少一个 |
1 | // 如果我们有 bat 或者 cat 至少一个 |
可以通过与掩码做或运算设置标志位,掩码中为 1 的位可以设置对应的位。例如掩码 1100 可用来设置位 C 和 D:
1 | // 我们有 cat 和 duck |
可以通过与掩码做与运算清除标志位,掩码中为 0 的位可以设置对应的位。掩码可以通过对原语掩码做非运算得到。例如,掩码 1010 可以用来清除标志位 A 和 C :
1 | // 我们没有 ant 也没有 cat |
如上的掩码同样可以通过 ~FLAG_A & ~FLAG_C 得到(德摩根定律)
1 | // 我们没有 ant 也没有 cat |
标志位可以使用异或运算切换。所有值为 1 的位可以切换对应的位。例如,掩码 0110 可以用来切换标志位 B 和 C:
1 | // 如果我们以前没有 bat ,那么我们现在有 bat |
最后,所有标志位可以通过非运算翻转:1
2// entering parallel universe...
flags = ~flags; // ~1010 => 0101
转换片段
将一个二进制数的 String 转换为十进制的 Number:1
2
3var sBinString = "1011";
var nMyNumber = parseInt(sBinString, 2);
alert(nMyNumber); // 打印 11
将一个十进制的 Number 转换为二进制数的 String:1
2
3var nMyNumber = 11;
var sBinString = nMyNumber.toString(2);
alert(sBinString); // 打印 1011
自动化掩码创建
如果你需要从一系列的 Boolean 值创建一个掩码,你可以:
1 | function createMask () { |
逆算法:从掩码得到布尔数组
1 | function arrayFromMask (nMask) { |
位运算的应用
按位非~判断索引存在
一般都是用“str.indexOf(‘test’) > -1”这种形式来判断字符串str中是否包含”test”字符串,现在可以利用位运算符“~”:“~str.indexOf(‘test’)”,包含时返回非0数字,不包含时则返回0。
时间对比: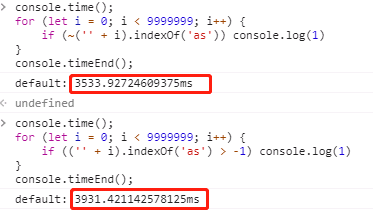
其实两者执行性能差距不大。
再来简单介绍下用~判断索引的原理,核心:1
~-1 === 0
-1在内存的表示的二进制符号全为1,按位非之后就变成了0. 由此也说明了-1在内存的表示为:0000…0001,第一位0表示符号位为正,如果是-1的话符号位为负用1表示1000…0001,这个是-1的原码,然后符号位不动,其余位取反变成1111…1110,这个就是-1的反码表示,反码再加1就变成了1111…1111,这个就是-1的补码,负数在内存里面(机器数)使用补码表示,正数是用原码。所以全部都是1的机器数按位非之后就变成了全为0。剩下的其它所有数按位非都不为0,所以利用这个特性可以用来做indexOf的判断,我个人已经习惯这种写法,因为感觉更方便并且代码看起来更简洁。
判断数字奇偶性:&
1 | 奇数 & 1 = 1; |
如1
2
3
4
5var num1 = 10,
num2 = 13;
console.log(num1 & 1); // 0
console.log(num2 & 1); // 1
取整(舍弃小数部分):~~/>>/<</>>>/|
注:>>>不可用于负数。
如1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43// 正数
console.log(~~5.21); // 5
console.log(5.21 >> 0); // 5
console.log(5.21 << 0); // 5
console.log(5.21 | 0); // 5
console.log(5.21 >>> 0); // 5
// 负数
console.log(~~-5.21); // -5
console.log(-5.21 >> 0); // -5
console.log(-5.21 << 0); // -5
console.log(-5.21 | 0); // -5
console.log(-5.21 >>> 0); // 4294967291,所以不可使用>>>对负数进行取整
// 字符串正数
console.log(~~'5.21'); // 5
console.log('5.21' >> 0); // 5
console.log('5.21' << 0); // 5
console.log('5.21' | 0); // 5
console.log('5.21' >>> 0); // 5
// 字符串负数
console.log(~~'-5.21'); // 5
console.log('-5.21' >> 0); // 5
console.log('-5.21' << 0); // 5
console.log('-5.21' | 0); // 5
console.log('-5.21' >>> 0); // 4294967291,所以不可使用>>>对字符串负数进行取整
// 空字符串
console.log(~~''); // 0 同其他
// boolean
console.log(~~true); // 1 同其他
console.log(~~false); // 0 同其他
// undefined
console.log(~~undefined); // 0 同其他
// null
console.log(~~null); // 0 同其他
// NaN
console.log(~~NaN); // 0 同其他
>>实际上是一个快速的Math.floor()函数,速度有提升。
经典题,数字交换
要求不能使用额外的变量或内容空间来交换两个整数的值。使用异或位运算可以达到这个目的。
1 | var a = 1, |
为什么a ^ a = 0, b ^ b = 0呢?1
2
3
4 01011010
^ 10010110
-----------
11001100
异或的运算过程可以当作把两个数加起来,然后进位去掉,0 + 0 = 0,1 + 0 = 1,1 + 1 = 0。这样就很好记。所以a ^ a在所有二进制位上,要么同为0,要么同为1,相加结果都为0,最后就为0.
异或也常被用于加密。
使用按位与&去掉高位
去操作数的高位,只保留低位,例如有a, b两个数:
1 | let a = 0b01000110; // 十进制为70 |
现在认为他们的高位是没用的,只有低4位是有用的,即最后面4位,为了比较a,b后4位的大小,可以这样比较:
1 | a & 0b00001111 < b & 0b00001111 // true |
a, b的前4位和0000与一下之后就都变成0了,而后四位和1111与一下之后还是原来的数。这个实际的作用是有一个数字它的前几位被当作A用途,而后几位被用当B用途,为了去掉前几位对B用途的影响,就可以这样与一下。
另外一个例子是子网掩码,假设现在我是网络管理员,我能够管理的IP地址是从192.168.1.0到192.168.1.255,即只能调配最后面8位。现在把这些IP地址分成6个子网,通过IP地址进行区分,由于6等于二进制的110,所以最后面8位的前3位用来表示子网,而后5位用来表示主机(即总的主机数的范围为00001 ~ 11111, 共30个)。当前网络的子网掩码取为255.255.255.111 00000即255.255.255.224,假设某台主机的IP地址为192.168.1.120,现在要知道它处于哪个子网,可以用它IP地址与子网掩码与一下:120 & 224 = 96 = 0b 011 00000,就知道它所在的子网为011即3号子网。
这个是保留高位去掉低位的例子,刚好与上面的例子相反。
使用按位|构造属性集
Google地图中有个骚操作,利用位操作来判断位置,即边界判断。
边界判断的例子——要在当前鼠标的位置往上弹一个悬浮框,如下图左所示,但是当鼠标比较靠边的时候就会导致悬浮框超出边界了。
为此,需要做边界判断,总共有3种超出情况:右、上、左,并且可能会叠加,如鼠标在左上角的时候会导致左边和上面同时超出。需要记录超出的情况进行调整,用001表示右边超出,010表示上方超出,100表示左边超出,如下代码计算:
1 | //右边超出 |
如果左边和上面同时超出,那么通过或运算2 | 4 = 6,得到6 = 0b110. 就知道了超出的情况,这样的代码相对于在if里面写两个判断要好一些。
使用按位与&进行标志位判断
现在有个后台管理系统,操作权限分为一级、二级、三级管理员,其中一级管理员拥有最高的权限,二、三级较低,有些操作只允许一、二级管理员操作,有些操作只允许一、三级管理员操作。现在已经登陆的某权限的用户要进行某个操作,要用怎样的数据结构能很方便地判断他能不能进行这个操作呢?
我们用位来表示管理权限,一级用第3位,二级用第2位,三级用第1位,即一级的权限表示为0b100 = 4,二级权限表示为0b010 = 2,三级权限表示为0b001 = 1。如果A操作只能由一级和二级操作,那么这个权限值表示为6 = 0b110,它和一级权限与一下:6 & 4 = 0b110 & 0b100 = 4,得到的值不为0,所以认为有权限,同理和二级权限与一下6 & 2 = 2也不为0,而与三级权限与一下6 & 1 = 0,所以三级没有权限。这里标志位的1表示打开,0表示关闭。
这样的好处在于,我们可以用一个数字,而不是一个数组来表示某个操作的权限集,同时在进行权限判断的时候也很方便。
不使用加减乘除来做加法
(经常用来考察对位运算的掌握情况)
不能用加减乘除,意思就是要你用位运算进行计算。以实际例子说明,如a = 81 = 0b1010001,b = 53 = 0b0110101。通过异或运算,我们发现异或把两个数相加但是不能进位,而通过与运算能够知道哪些位需要进位,如下所示:
1 | 1010001 |
把通过与运算得到的值向左移一位,再和通过异或得到的值相加,就相当于实现了进位,这个应该不难理解。为了实现这两个数的相加可以再重复这个过程:先异或,再与,然后进位,直到不需要再进位了就加完了。所以不难写出以下代码:
1 | function addByBit(a, b) { |
位运算还经常用于生成随机数、哈希,例如Chrome对字符串进行哈希的算法是这样的:
1 | uint32_t StringHasher::AddCharacterCore(uint32_t running_hash, uint16_t c) { |
不断对当前字符串的ASCII值进行累加运算,里面用到了异或,左移和右移。
位掩码来判断选项
1 | // 定义所有的可选项 |
Author
My name is Micheal Wayne and this is my blog.
I am a front-end software engineer.
Contact: michealwayne@163.com